Quantum tensor networks
Computational complexity makes the interacting quantum many-body systems hard to simulate efficiently on a classical computer. The main obstacle stems from their huge Hilbert space, which is growing exponentially with the number of particles. A remarkable example is the Hubbard model of strongly interacting electrons on a two-dimensional square lattice. Th relatively simple-looking model, relevant for high-Tc superconducting materials, was formulated over 40 years ago. Still, despite an enormous analytical and numerical effort, some of the most fundamental questions, including the existence of stripe phases or the very superconductivity itself, have not been settled yet.
One of the most promising approaches to efficiently simulate quantum many-body systems on classical computers are quantum tensor network algorithms. Originating in studies of statistical and condensed matter systems, nowadays, they are finding applications in numerous fields ranging from quantum computation to machine learning.
Our group is actively pushing the boundaries of tensor network methodology with applications including simulations of fermionic matter in two dimensions at finite temperature, non-equilibrium quantum many-body dynamics, quantum transport, or optimization/spin-glass physics.
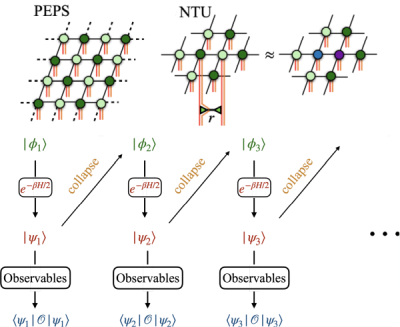Fig. 1. Two strategies to study the fermionic Hubbard model via projected entangled-pairs states tensor network. In the top row: imaginary time evolution of a purification of density matrix at finite temperature. In the bottom row, the Markov chain Monte Carlo within minimally-entangled typical thermal states approach, combined with PEPS ansatz and neighborhood tensor update. The latter trades the PEPS bond dimension and memory with sampling to open new simulation opportunities in this prototypical problem.
From: A. Sinha, M. M. Rams, P. Czarnik and J. Dziarmaga, Phys. Rev. B 106, 195105 (2022). A. Sinha, M. M. Rams and J. Dziarmaga, arxiv:arXiv:2310.08533
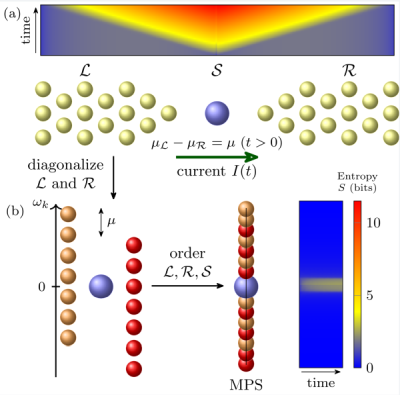Fig. 2. Entanglement, transport, and simulation. (a) A bias or particle imbalance between the L and R reservoirs drives a current I through the impurity system S. This spatial structure, though, has an entanglement light cone (over top heat map), leading to macroscopic entanglement and simulation failure. (b) Separately diagonalizing the single-particle eigenstates in the L and R regions and combining them into a joint LR environment circumvents this issue by naturally structuring the simulated system. The entanglement then becomes localized within the bias window and highly suppressed (right heat map), breaking the entanglement barrier and allowing non-equilibrium many-body simulations that are extensive in system size and evolution time.
From: M. M Rams and M. Zwolak, Phys. Rev. Lett. 124, 137701 (2020).
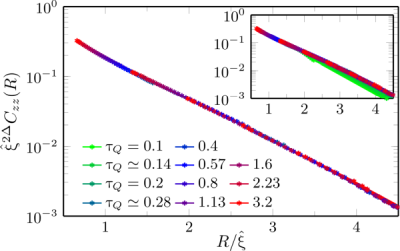Fig. 3. Kibble-Zurek dynamical scaling of ferromagnetic correlation functions in 2D quantum Ising model. A system prepared in the ground state and quenched across a quantum critical point at a finite rate gets excited, with universal features of such a transition predicted by the Kibble-Zurek mechanism. A scaling collapse in the plot corroborates the mechanism in 2D quantum matter. Result for infinite lattice employing projected entangled-pairs states ansatz and neighborhood tensor update.
From: M. Schmitt, M. M. Rams, J. Dziarmaga, M. Heyl and W. H. Zurek, Sci. Adv. 8, eabl6850 (2022).
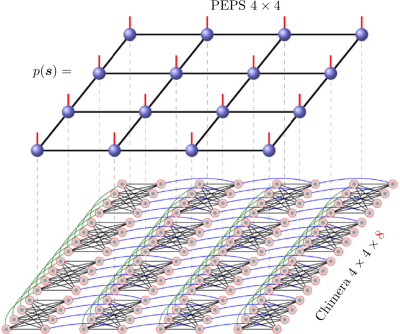Fig. 4. The probability distribution of possible configurations of the random Ising spin-glass instance is represented as a PEPS tensor network. Approximated network contractions, combined with a branch and bound algorithm, allow searching for the ground state and encoding the structure of the low-energy spectrum of this optimization problem.
From: M. M. Rams, M. Mohseni, D. Eppens, K. Jałowiecki and B. Gardas, Phys. Rev. E 104, 025308 (2021).
Acknowledgments
This line of reaserch in our group has been supported by a number of NCN grants:
- Sonata Bis Quantum tensor networks: From spin glasses to quantum transport 2021-26
- Opus Quantum tensor networks for strongly correlated systems 2020-24
- QuantERA NAQUAS: Non-equilibrium dynamics in Atomic systems for QUAntum Simulation 2018-22
- Opus Classical and quantum computation of strongly correlated systems 2017-20